Глава 7
В которой мы обучаем Черепашку рисовать окружности и дуги и вспоминаем про замечательное число 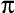 , с помощью которого еще древние греки определяли длину окружности по ее радиусу.
, с помощью которого еще древние греки определяли длину окружности по ее радиусу.
"И сделал литое из меди море, — от края его до края его десять локтей, — совсем круглое… и снурок в тридцать локтей обнимал его кругом"
(3 Цар.7.23)
Мы уже убедились в том, что 360-угольник или 180-угольник или даже 60-угольник вполне могут служить нам моделью окружности. Наш глаз не замечает "неровностей" их контура. Эти многоугольники можно нарисовать, используя, например, команды
Но при такой записи, задавая наугад длину стороны многоугольника, трудно представить, какая именно окружность получится.
Мы знаем, что у окружности есть очень важная характеристика — ее радиус. Как рассчитать длину стороны многоугольника, заменяющего нам окружность, в зависимости от радиуса R этой окружности?
Еще в Древней Греции ученые знали, если измерить длину окружности и затем разделить полученное значение на длину диаметра (а он равен двум радиусам), то для любой окружности — маленькой, большой, крохотной или громадной — получится одно и то же число, близкое к трем, которое они обозначили 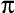 (читается: “пи”).
(читается: “пи”). 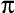 — замечательное число, равное приблизительно 3,1415926 и получившее свое название по первой букве греческого слова “периферия” (“окружность”). Используя
— замечательное число, равное приблизительно 3,1415926 и получившее свое название по первой букве греческого слова “периферия” (“окружность”). Используя 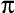 , можно записать:
, можно записать:
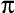 R,
R, 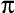 - замечательное число, равное приблизительно 3,1415926
- замечательное число, равное приблизительно 3,1415926
В Лого не обязательно помнить значение числа 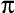 , Черепашка понимает его обозначение — pi, которое можно применять в формулах.
, Черепашка понимает его обозначение — pi, которое можно применять в формулах.
Теперь у нас достаточно идей для построения окружности. Действительно, пусть мы хотим нарисовать окружность радиуса, например, 50. Длина такой окружности составит 2 * pi * 50 (черепашьих шагов). В Лого окружность мы заменяем многоугольником и в этом случае 2 * pi * 50 есть периметр этого многоугольника. Тогда для 360-угольника длина стороны составит 2 * pi * 50 / 360, для 180-угольника — 2 * pi * 50 / 180, для 60-угольника — 2 * pi * 50 / 60. Используя "Закон 360-ти" нетрудно написать команды для рисования этих многоугольников:
repeat 180[fd 2 * pi * 50 / 180 rt 2] — 180-ти угольник
repeat 60[fd 2 * pi * 50 / 60 rt 6] — 60-ти угольник
Любой из этих многоугольников может служить моделью окружности радиуса 50.
Выберем для определенности 360-угольник и опишем его в виде процедуры
repeat 360[fd 2 * pi * 50 / 360 rt 1]
end
Если мы будем "проходить" не весь многоугольник, а только его часть, то получим соответствующие дуги:
| половина окружности: repeat 180[fd 2 * pi * 50 / 360 rt 1] end |
четверть окружности: repeat 90[fd 2 * pi * 50 / 360 rt 1] end |
| шестая часть окружности: repeat 60[fd 2 * pi * 50 / 360 rt 1] end |
треть окружности: repeat 120[fd 2 * pi * 50 / 360 rt 1] end |
Так можно описать любую дугу, являющуюся частью окружности. Не забудем при этом, что разные окружности имеют разные радиусы и, кроме того, окружности могут быть как “правыми”, которые Черепашка обходит, поворачиваясь направо после каждого шага, так и “левыми”. Соответственно и дуги могут быть как “правыми”, так и “левыми”:
| половина “левой” окружности радиуса 40: repeat 180[fd 2 * pi * 40 / 360 lt 1] end |
четверть “левой” окружности радиуса 80: repeat 90[fd 2 * pi * 80 / 360 lt 1] end |
 || Глава 6 ||
|| Вопросы и задания ||
|| Глава 8 ||
|| Глава 6 ||
|| Вопросы и задания ||
|| Глава 8 ||