The name of Bernoulli is well known not only among mathematicians. Many members of this remarkable Switzerland family became famous. Some of them were members of the Saint-Petersburg's Academy of Science, the city where we live.

Two brothers Jacob and Johann brought many new ideas to mathematics and phisics. Their nephew Nicolas, Johann's sons Nicolas and Daniel, Johann's grandsons Jacob and Johann were also well known scientists.

The spiral we are considering is named after Jacob Bernoulli.

Jacob Bernoulli was born on the 27th of December, 1654 in Basel, Switzerland and died there on the 16th of August, 1705. He graduated with a theology degree from Basel in 1676 and received training in mathematics and astronomy against the wishes of his parents. Among the curves that Jacob Bernoulli worked on were the Cycloid, the Epicycloid, the Equiangular spiral, the Hypocycloid and the Lemniscate which is now named after him.

It's interesting that Bernoulli's Lemniscate is used now in places when a tram makes a turn of a small radius.

There is a Crater Bernoulli on the moon (which is named after this mathematician and Johann Bernoulli).

Bernoulli's Spiral

Among early Greek mathematicians, the Pythagoreans firmly believed that everything could be explained in terms of numbers. They insisted that there was always some law involving numbers which characterized works of art, as well as living forms, creations of Nature. One of the best known of these ideas was the Law of the Golden Mean, or the Golden Section.

We meet this proportion in geometry when we divide a given line segment into two parts, a and b, such that a:b=b:(a+b), where a < b . The ratio b/a is named "tau" and is equal to the positive root of the equation , which is 1.618033989... It was called "Divine Propotion" (Luca Pacioli, fifteenth-century Italian mathematician and a friend of Leonardo da Vinci) and "one of the two Jewels of Geometry" (Kepler, the celebrated astronomer of the 17th century).

The Golden Mean appears at many unexpected turns, in the leaf arrangement on stems, or florets in flowers, Fibonacci series or Pentagon shapes, measurements of the human body or in spiral shapes of mollusks.

This fact we can use to build Bernoulli’s Spiral in a rather simple way.

Rectangles whose sides are in the ratio of "tau" to 1 are said to be of the shape most pleasing to the eye; they are called "golden rectangles".

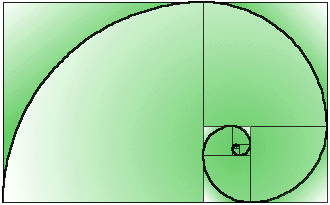
You may take it for granted or you may check it, that the golden rectangle can be dissected into two pieces: a square and a smaller golden rectangle. From the smaller rectangle we can cut off another square, leaving a still smaller rectangle and continue the process indefinitely. Quadrants of circles, inscribed in the successive squares, form a spiral, which is not just a Bernoulli’s spiral, but our eye can scarcely distinguish it from the real one.

Bernoulli’s spiral occurs naturally in many places like sea-shells where the growth of an organism is proportional to the size of the organism.

This "spira mirabilis" impressed so greatly the imagination of the famous mathematician, that he wished it to be carved on his tomb.

---

 Back to the Story One page    Spiral's model in Logo