
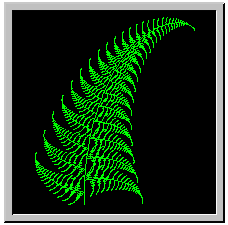
Now look attentively at this beautiful fern and let's take a part of it and look at it through the magnifier. The part of the fern is seen to bear a resemblance to the whole thing, isn't it? The likeness continuing with the parts of the parts and so on to infinity. These shapes are called fractals.The nature of fractals is reflected in the word itself, coined by mathematician Benoit B. Mandelbrot from the Latin verb frangere, "to break," and the related adjective fractus, "irregular and fragmented."
In 1967, Mandelbrot published an article in the journal Science entitled "How Long is the Coastline of Britain?" In this article, he showed that there is no correct answer to this question, because the more closely a coastline is examined, the more jagged - and thus longer - it appears. At every level of magnification above the molecular, the coastline looks irregular. Similar irregularities occur everywhere in nature, as Mandelbrot pointed out: "clouds are not spheres, mountains are not cones, coastlines are not circles, and bark is not smooth, nor does lightning travel in a straight line."
It's impossible to overestimate the significance of Mandelbrot's investigation of fractal shapes. It has influenced the whole 20th century science. Now scientists agree that nature is characterized more by irregularity and unpredictability than by their opposites and the events and objects' behaviour often can't be predicted precisely. Fractal models found their places in mathematics and physics, biology and geology, social life and, of course, art.
Computer-graphics specialists, using a recursive splitting technique, have produced striking new fractal images. Landscapes made this way have been used as backgrounds in many motion pictures; trees and other branching structures have been used in still lifes and animations.
Well, now I think, you are eager to try and make some fractals on your own. Of course, one should be a skilful programmer to design complex fractal shapes, but even simple ones may be eye catching. So, come on!
First two lessons on recursion
Back to the Main Menu | First Story. Spirals | Second Story. Wheels