Построение Золотого прямоугольника

«Золотым» называется прямоугольник, стороны которого находятся в отношении 1.618 к 1.

Это соотношение можно обнаружить и в архитектурных сооружениях, и в композициях живописных полотен, и в привычных предметах окружающего нас мира.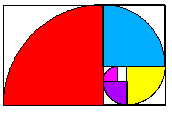

У «золотого» прямоугольника есть замечательное свойство: если «отрезать» от прямоугольника квадрат, то оставшаяся часть будет опять «золотым» прямоугольником, только меньшего размера. Вписывая четвертинки окружностей в «отрезаемые» квадраты, мы получим спираль, которая широко встречается в природе — в раковинах улиток и моллюсков, расположении семечек в подсолнухе и чешуек в хвойных шишках.

Построение «золотого» прямоугольника в программе Живая математика

1. Строим квадрат ABCD
2. Сторону AB делим пополам точкой E.
3. Строим окружность с центром в точке E и радиусом EC.
4. Нас интересует точка пересечения окружности с продолжением стороны AB за точку B. Эта точка — F — третья вершина искомого прямоугольника (первая — точка A, еще одна — D).
5. Восстанавливаем перпендикуляр в точке F к прямой AF.
6. Продлеваем DC до пересечения с перпендикуляром. Таким образом получаем третью вершину — G.
7. Прямоугольник построен.

По материалам статьи «Геометрия Фибоначчи» (www.alpari-idc.ru/ru/elliott-wave/l17.html)

Наверх